Proximity Search using Quadtrees
By:
Vineet Puranik
On
12/06/2023Reading time:
12 min
Proximity search is a fundamental aspect of applications like food delivery and rider sharing services. Its primary objective is to find nearby entities based on a given reference location. In this article, we will delve into the implementation of proximity search using an efficient data structure called Quadtree. By leveraging the power of Quadtrees, we can enhance the speed of proximity searches in these applications. We will start off by establishing our problem statement. Then we will approach the proximity search solution using a naive search and a Quadtree solution. Finally, we will compare both the solutions and inspect how Quadtrees help us in gaining a significant speedup compared to the naive search solution.
Problem statement
Say we represent the map of the earth in a 2D space. This 2D space contains all the locations of interest for our proximity search use case. Each location can be modelled as a "point" (all the points in the image below) in the 2D space using x and y co-ordinates (usually a derivation of the latitude and longitude values). Any point that falls within a boundary (dotted square region in the image below) surrounding the reference point (orange point in the image below) would be categorized as a nearby point (green points are nearby points). Our goal is to find all the points nearby to a reference point.

2D Space : Restaurants and User
To map the problem statement to a practical use case we can consider that all the points except the orange point correspond to restaurants. The orange point corresponds to the user's location. The search boundary is constructed using the user's location and the goal is to find all the restaurants that fall within the search boundary represented by green points within the search boundary .
Naive search solution
A naive search solution for our problem statement would be to store all the points in our 2D space that corresponds to the restaurants in a list and iterate over the list. In each iteration, we will check if the x and y co-ordinates of the restaurant fall within the bounds of the search boundary. Each restaurant that matches our check will be added to a list. After all the iterations the list will contains all the restaurants nearby the user's location. This solution has a time complexity of O(n) since we are performing the boundary check on each and every restaurant in our 2D space.
// points correspond to all the restaurants in our 2 dimensional space
// boundary represents the rectangular search region
// the function returns all the points contained in the rectangular search region
fn naive_search(points: &[Point], boundary: &Boundary) -> Vec<Point> {
points
.iter()
.filter(|&point| contains(boundary, *point))
.cloned()
.collect()
}
The solution will definitely not scale when we are dealing with millions and billions of restaurants in our 2D space. So, now the question is do we need to check each and every restaurant in our 2D space .. No. We can divide our 2D space into multiple sections. This will mean that our restaurants will be divided across these sections. Then for our search we can perform the boundary check for restaurants only on sections that intersect with the search boundary.

2D Space divided into 4 sections
Quadtrees
A Quadtree is a type of tree that is used to partition a 2D space by recursively subdividing it into 4 quadrants or regions. This subdivision occurs when a node of the Quadtree reaches the specified capacity for the number of points it can contain. The subdivision process involves spawning 4 child nodes for the given node followed by distribution of the existing points in the node across all the child nodes. The child nodes are then recursively subdivided once the number of points in those nodes reach the specified capacity. This recursive subdivision of nodes into 4 child nodes corresponds to the recursive subdivision of a 2D space into 4 quadrants.
For implementing our problem statement, we will define each node of our Quadtree to have the following properties :
boundary : represents the boundary of the current node (for the root node this will be the entire 2D space)
points : list of points that are stored in the current node. (restaurants)
top_left_child, bottom_left_child, top_right_child, bottom_right_child : pointers to 4 child nodes.
// Boundary defines an enclosed rectangular area.
struct Boundary {
x1: f64,
x2: f64,
y1: f64,
y2: f64,
}
// Quadtree is a tree where each node in the tree will have exactly 4 children.
// Each node will contain points upto 'MAX_CAPACITY'
// Once the number of points in a node have reached capacity, the node will be subdivided into 4 child nodes and all the points will be distributed to the child nodes
struct Quadtree {
boundary: Boundary,
points: Vec<Point>,
top_left_child: Option<Box<Quadtree>>,
bottom_left_child: Option<Box<Quadtree>>,
top_right_child: Option<Box<Quadtree>>,
bottom_right_child : Option<Box<Quadtree>>,
}
The construction of a Quadtree starts from an empty 2D space which will be the root node of the tree. As we insert points to our 2D space they will be associated with the root node of the Quadtree.

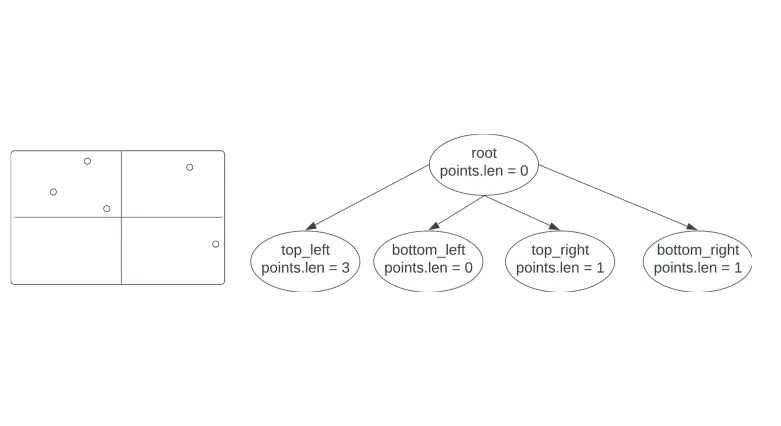
2D space (4 points) and Quadtree (capacity 4)
Let us consider that the defined capacity for the number of points a node can contain is 4. Once the number of points in the root node are exceeding the defined capacity (the insertion of the 5th point to the Quadtree will trigger this), it splits up into 4 child nodes and distributes existing points across these child nodes. Notice the length of the points list for each child.
2D space (5 points) and Quadtree (capacity 4)
Following the subdivision of the root node, new points added to the Quadtree will be added to the corresponding child node based on where the point lies in the divided 2D space. Once any child node is exceeding the defined capacity it will undergo the process of subdivision into 4 child nodes followed by distribution of the existing points across these child nodes. Consider the next 2 points falls within the top_left quadrant. As a result, it will be further subdivided into 4 child nodes since the capacity of the number of points contained in the node exceeds 4. The key fact is that every node will be split up into exactly 4 children nodes once they reach the defined capacity.

2D space (7 points) and Quadtree (capacity 4)
Using all the restaurants (points) in our 2D space, we will construct an in memory Quadtree data structure. This will be used to execute our search for nearby restaurants given the user's location and constructing the search boundary. Below is the rust code for the insert function.
fn insert(node: &mut Quadtree, point: Point) -> bool {
// check if the point is outside the node's boundary, if yes then return false
if !contains(&node.boundary, point) {
return false;
}
// if node has not reached capacacity and has not been sub-divided, insert the point in this node
if node.points.len() < MAXCAPACITY && node.top_left_child.isnone() {
node.points.push(point);
return true;
}
// if we reach here, that means there could be 2 possibilities
// 1. the node has already been sub-divided or
// 2. the node has reached its capacity but has not been sub-divided
// if node has reached its capacity but has not yet been sub-divided, we need to sub-divide
if node.top_left_child.is_none() {
subdivide(node);
}
// Insert the point into its correct child node.
// We can try inserting into all the child nodes
// The node where the point's position is outside the boundary would
// return false, until we find the correct child node.
if insert(node.top_left_child.as_mut().unwrap(), point) {
return true;
}
if insert(node.bottom_left_child.as_mut().unwrap(), point) {
return true;
}
if insert(node.top_right_child.as_mut().unwrap(), point) {
return true;
}
if insert(node.bottom_right_child .as_mut().unwrap(), point) {
return true;
}
false
}
Using Quadtrees, we will end up searching only those nodes whose boundaries intersect with the search boundary. This will enable us to skip nodes that are not relevant to our search boundary and thus we do not end up checking whether every restaurant in our 2D space falls within the search boundary. Below is the rust code for the search function.
// search returns all the points within the given boundary
fn search(node: &Quadtree, boundary: &Boundary) -> Vec<Point> {
// if this node does not interesect with the search boundary
// we know that the node and all its child nodes do not contain any points
// that fall in the search boundary
if !intersects(&node.boundary, boundary) {
return vec![];
}
// If this node has not yet been subdivided, return
// all the points within the search boundary
if node.top_left_child.is_none() {
return node
.points
.iter()
.filter(|&point| contains(boundary, *point))
.cloned()
.collect();
}
// If the node has been subdivided, search all
// the child nodes and merge the results
let mut result: Vec<Point> = Vec::new();
result.extend(search(node.top_left_child.as_ref().unwrap(), boundary));
result.extend(search(node.bottom_left_child.as_ref().unwrap(), boundary));
result.extend(search(node.top_right_child.as_ref().unwrap(), boundary));
result.extend(search(node.bottom_right_child .as_ref().unwrap(), boundary));
result
}
For a complete implementation of proximity search using both the naive search and Quadtrees in Rust, check out the git repository.
The effective time complexity for proximity search using Quadtrees is O(log n). This also depends on how the points are distributed across the 2D space. If there are only a few nodes that hold most of the nodes, then our Quadtree will unbalanced and the time complexity will tend closer to O(n).
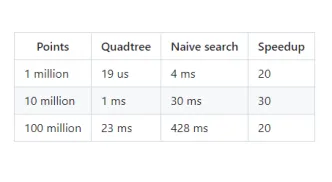
Timing Quadtree vs Naive search
Timing both the solutions for searching a provided search boundary across 10 runs using a set of 1 million, 10 million and 100 million points yielded the following results. The results clearly demonstrate that the Quadtree implementation is 20 to 30 times faster than the naive search solution. Note that the results may vary based on the configuration of the machine used to time the solutions.
Timing Quadtree vs Naive search
GitHub implementation:
https://github.com/vineetpuranik/rusty_quadtree
References: